Optimal Taxation Literature

Ramsey Model

The overall elasticity of a good is the percent equilibrium quantity changes due a percent change in price from taxes. You can compute this from the elasticity of demand ($\epsilon_d$) and supply ($\epsilon_s$) using this formula:

Ramsey proved that if you're levying flat consumption taxes, then the tax on each good should be inversely proportional to the elasticity of that good to minimize deadweight loss A Contribution to the Theory of Taxation.

This system obviously ignores redistributive goals and is probably regressive since necessities tend to be inelastic while luxury goods tend to be elastic.

Diamond extends this result from optimizing merely efficiency to optimizing social welfare as a whole. He determined that the if we still restrict ourselves to flat consumption taxes, the optimal rate on each good should be multiplied by the average marginal utility for consumers of that good A many-person Ramsey tax rule.

Land Value Tax

As a special case of the Ramsey rule, perfectly inelastic goods and services should be taxed to the greatest extent possible. This is the main impetus behind a land value tax - taxing the value of all land but not the value of any improvements made to it (e.g. buildings).

The logic is simply that since the supply of land is perfectly inelastic (well mostly Land reclamation), a tax on land has zero dead-weight loss and is therefore optimal from an efficiency standpoint. In fact, from this perspective, we can levy a tax equal to the entire value of the land times the interest rate, effectively giving the government all income derived from unimproved land - all without any efficiency trade-off.

Another reason the tax tends to be popular is that its progressive since the poor tend to own no land at all. A skeptic may think landlords will just raise rents, but since the supply is perfectly inelastic, the entire incidence of the tax should fall on landlords rather than renters.

Finally, if your unimproved plot of land gains value, it's because other people improved the land around you. This makes that value an externality and makes you essentially a rent seeker. A 100% land value tax removes this unfair value people get when they luck out and their land becomes more valuable through no actions of their own.

There are also arguments against:

• It's difficult to assess how much a piece of land would be worth without any improvements.
• If land values increase around you, you may be unable to afford the land value tax and will, thus, be forced from your home.
• A land value tax is unnecessary to the extent the Atkinson-Stiglitz result holds (discussed later).

Laffer Curve (Flat Income Tax)

Instead of optimizing for social welfare, what if we want to optimize for tax revenue? For simplicity, we'll consider a flat tax example.

First of all, it is obvious that revenue will be zero at t=0 since there is no tax. It is nearly as obvious that revenue will be zero at t=1, since no one will work if the tax rate is 100%. Assuming some revenue can be raised, it therefore follows the revenue-maximizing rate is between 0% and 100%.

Let $\epsilon$ be the the elasticity of income with respect to $1-t$. For instance, if $\epsilon=0.4$, then increasing taxes from 0% to 1% will cause income to decrease by 0.4%.

Given the above, we can show that maximum tax revenue is given by

Using our arbitrary example of $\epsilon=0.4$, this implies a revenue-maximizing rate of ~71%.

The traditional interpretation is that you never want to have rates above the revenue-maximizing rate, since such rates harm both the government's ability to help society and also harm the person being taxed. In principle, (and maybe in practice), you could justify a higher tax rate if you actually want to discourage working.

The Mirrlees Model (Income Taxes)

Suppose consumption is given by $c = w L - T(w L)$, where $w$ is your wage, $L$ is your labor, and $T(w L)$ is how much you pay in taxes.

Also, suppose everyone has the same utility function $u(c, L)$ where $c$ and they're trying to maximize it:

Finally, suppose there are $h(w)$ people with wage $w$ and that the government has its own social welfare function $G$ such that it is optimizing for

but it needs to raise enough revenue to match our expenditures, $E$:

Two notes:

1. Conventional utilitarianism suggests $G(x)=x$. However, both unconventional utilitarians (e.g. Rawlsian ones) and conventional utilitarians who believe people optimize for the wrong things should choose a non-trivial $G$.
2. This model is premised on the assumption that the only reason we don't perfectly redistribute income is due to behavioral responses. Some people argue that at least some people intrinsically deserve at least some of their income.

From this approach, a few general results have been proven:

• Taxes should be negative at low incomes.
• Taxes should positive at high incomes.
• Marginal tax rates should never be negative Seade.
• Marginal tax rates should never be above 100% (trivial since no one would work).
• The marginal tax rate on the very highest earner should be zero if the skill distribution is bounded Sadka. This result is generally believed to be inapplicable to reality as we'll discuss in a bit.

Suppose the maximum tax bracket has rate $\tau$ and is applied to all income above $\bar{z}$. Suppose there are $N$ people who earn above that and that their average income is $z_m$.

If I increase $\tau$, this

1. increases tax revenue simply due to having a higher tax rate
2. reduces tax revenue by discouraging labor
3. reduces the welfare of these $N$ people by making them consume less

These three effects are called the fiscal effect, the behavioral effect, and the welfare effect. I won't really discuss them more, but they come up a lot in the literature and are the sources of some of the derivatives I merely state later on.

We can represent this mathematically using the derivative of social welfare with respect to $\tau$:

where $g$ represents how much.

We can optimize by setting this derivative to zero to achieve Using elasticities to derive optimal income tax rates:

Note, these results make intuitive sense:

• As $g$ increases, $\tau$ should decrease.
• As $\epsilon$ increases, $\tau$ should decrease.
• As $z_m/\bar{z}$ increases, income inequality increases, and $\tau$ increases.

A couple things to note:

• This formula is less precise than it appears. Most people believe, for instance, that changes to the top tax rate will affect $z^m$ and $\epsilon$

• This result can also be used to show both (1) that the top earner should face a 0% marginal tax rate and (2) that this "proof" is completely inapplicable to reality.

  Basically, for the top earner, as $\bar{z}$ approaches their income, the optimal $\tau$ goes to zero. Hence, if we were to implement a tax bracket just below the top earner's income, that bracket's rate should be 0%.

  In English, the basic argument goes "if we can predict the top earner's income, we can introduce a new 0% tax bracket just below to encourage them to work more with virtually no revenue loss."

  However, this entire paradigm is inapplicable to reality, because we cannot (in fact) predict the top earner's income very well. If, for instance, the top bracket's threshold is half the top earner's income, this entire argument utterly breaks down.

• As a special case, we can reproduce the Laffer curve result by letting $\bar{z}=0$ and $g=0$.

After proving this, Saez uses this model to argue the optimal top tax rate is between 50% and 80% Using elasticities to derive optimal income tax rates.

Let's generalize this to non-linear income taxes.

Consider the people earning between $z$ and $z+dz$. If I change their marginal tax rate by a small amount, we can use the derivative of social welfare relative to their marginal tax rate to compute the change in their welfare:

where $H$ is the CDF of income (as $h$ was the pdf).

When we set this to zero, we get

Note, this result requires us to assume that labor decisions are only made based on the marginal tax rate. This is almost certainly false.

One note on the $(1-H(z))/h(z)$ term. This term implies that when few people are earning $z$ income and lots of people are earning above $z$, the marginal tax rate at $z$ should be high. The intuitive reason is that our distortion is low (few people pay the high marginal tax), but it lets us raise effective rates on everyone above that point without discouraging their labor.

Although we can't elegantly solve for the entire tax system, we can solve for the best system computationally based on the current US tax system and income distribution. Saez did this Using elasticities to derive optimal income tax rates. The review of economic studies and found:

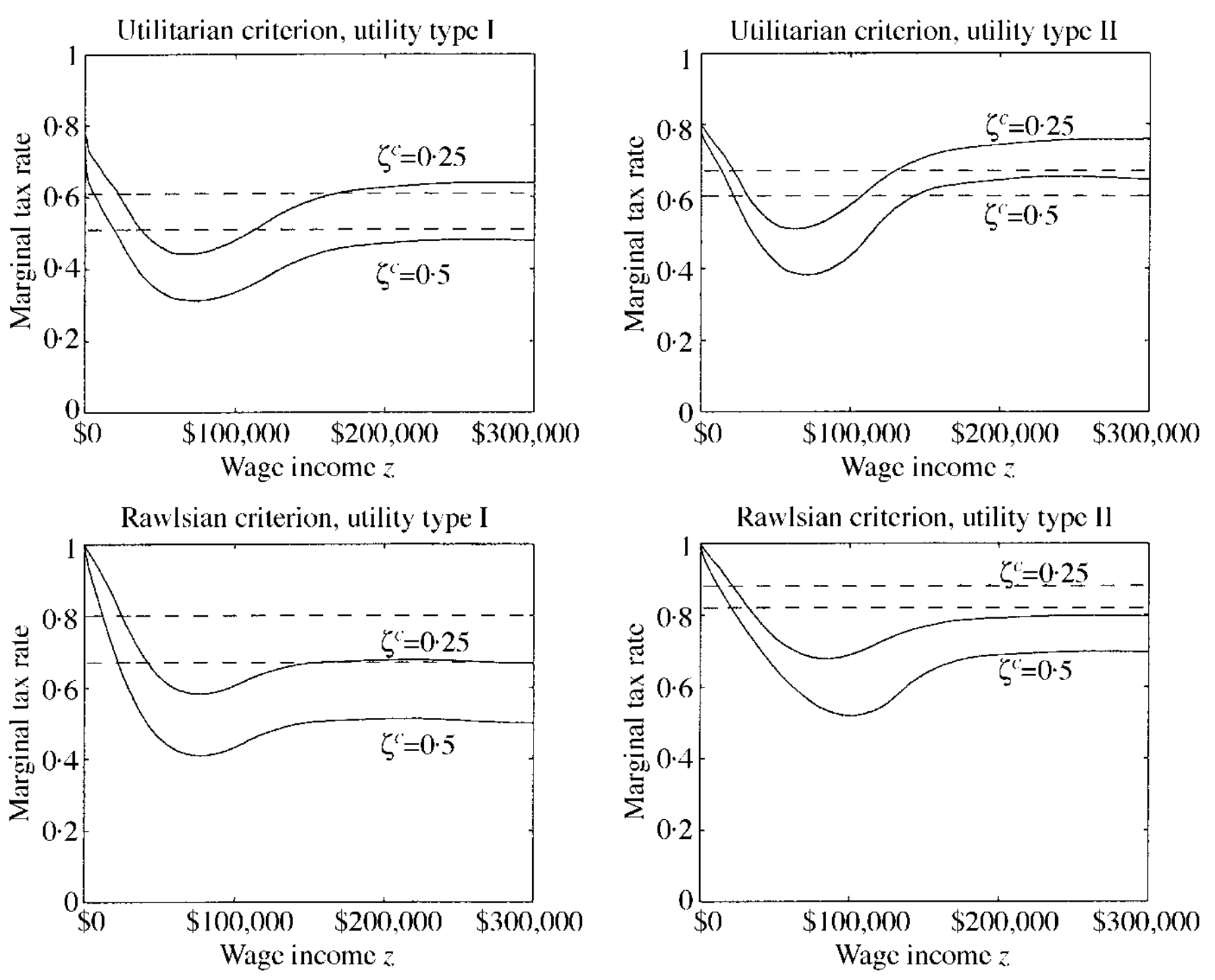
TODO: Diamond 1998, Piketty 1997

Discrete Labor Model

One of the problems with the Mirrlees model is that it assumes people can choose any number of hours, when, in reality, it is difficult to work, say, 4 hours per week. Instead, people are likely to respond to taxes and transfers by dropping in or re-entering the workforce.

Suppose we have a finite number of jobs and each individual is trained for only one of those jobs and all people working the same job earn the same wage. Each individual can merely choose whether or not to work and the government can choose to levy a tax on each job. Finally, suppose that if after-tax income goes down by 1%, the participation rate of a job goes down by some fixed percent.

This model implies that work subsidies are optimal Optimal income transfer programs: intensive versus extensive labor supply responses - directly contradicting our earlier result that the marginal tax rate never be negative. This justifies programs like the EITC.

Saez finally combines both the Mirrlees and the discrete labor model into a single general model, but that is more complicated, so we won't go into it other than to say that this can still support negative marginal tax rates at low incomes.

Capital Gains Taxation

What To Tax?

Odds and Ends

Cash vs In-Kind Transfer

Naively, theory suggests governments should prefer cash transfers to in-kind transfers (e.g. food stamps, housing vouchers, etc). The arguments for this is straightforward: (1) the person receiving the welfare knows what they need better than the government and (2) cash transfers are easier/cheaper for both the government and the recipient to handle.

However, some economists argue that in-kind transfers have their place Nichols. For instance, suppose you have a soup kitchen that requires waiting in line to get soup.

A poor person might get 2 utils from soup and might lose 1 util from waiting, so they choose to wait in line for free soup.

A rich person might get 1 util from soup (they can easily afford better food) and lose 2 utils from waiting, so they choose not to wait in line for free soup.

In this way, in-kind transfers can closely target the people who have more free time relative to income (i.e. the poor).

There are some theoretical situations where cash transfers work better and others where in-kind transfers work better. Which is better in the real world depends a great deal on the specific situation.

Tax Incidence

One issue with periodic (i.e. monthly) welfare payments is that they cause a temporary surge in demand, which firms can take advantage of by raising prices.

For instance, even though it is illegal for companies to price-discriminate based on whether purchases are made with food-stamps, the fact that food-stamps are paid out at the beginning of the month means that the food-stamps program causes a ~30% surge in demand for food during the beginning of the month in high food-stamp areas. Presumably for this reason, stores raise prices at the beginning of the month by ~2.5%. In this way, some of the social welfare created by food stamps makes its way to the stores rather than the intended recipients Hastings. Conversely, people who don't receive food-stamps are also hurt by the higher prices.

Note, that if everyone received food stamps (to destigmatize them), this effect would be significantly larger because (1) we'd see a larger surge and (2) while companies have limited ability to change their prices "optimally" now because even in high food-stamp areas, the vast majority of customers aren't using food stamps, this limitation would cease.

Conversely, this demonstrates that, today, legally requiring that food stamps be treated as cash largely prevents firms from taking reaping the benefits from this social program for themselves. In a similar way the fact that the EITC only applies to workers with kids helps prevent employers from taking its money; likewise, some people believe that EITC causes general wage cuts, so non-EITC workers end up being hurt Rothstein.

An alternative approach to estimate the effect of tax/welfare policy is to look at how asset prices change when a policy is announced. (see for example Friedman).

Finally, it's worth pointing out that mandates are very different than taxes. For instance, if the government implements a 10% payroll tax to pay for a healthcare program, we'd expect firms and laborers to both bear some of that tax while the unhealthy benefit. In the Mirrlees labor model, this will reduce total hours worked.

However, if the government mandates that employers pay for healthcare and make it illegal to discriminate based on health, then we'd expect (for the most part) employees to bear the brunt of the cost via lower pay, but we wouldn't expect their overall compensation to fall. Likewise, it's entirely possible in the Mirrlees labor model that total hours worked won't change.

In particular, if an employee values the mandated benefit at $\alpha$ times its cash cost, the distortion's size is $(1 - \alpha)$ times what achieving the mandate with a tax would be.

Salience

todo Salience and taxation: Theory and evidence

Philosophical Considerations

Philosophically, you can think of redistributive concerns as "insurance behind a veil of ignorance". However, you can also justify progressive taxation as "insurance in front of a veil of ignorance." The basic idea is that if you face an adverse event (e.g. you become blind), a progressive tax system makes it so you have to reduce your consumption by less than you otherwise would have. See Varian for a more mathematical analysis.