Corporate Taxation

The Neoclassical Model

Let's assume we have a CEO that is purely trying to maximize shareholder value. Furthermore, let's suppose they sell shares to raise $E$ dollars this year, and buy all the shares back next year for $E$ plus $D$ in dividends. Then, the net present value of the firm is

where $X$ is money the firm already has, $r$ is the interest rate, $\tau_d$ is the tax rate on dividends, $\tau_c$ is the tax rate on corporate profits, and $f$ is a function that represents the returns the company gets by investing their money.

Fundamentally, there are two kinds of firms: cash-rich ones and cash-constrained ones. The former have enough cash to satisfy any investment options they have that yield above the market interest rate. The latter do not and so borrow from investors.

Cash-rich firms never issue new equity ($E=0$) and splits all profit into dividends and investment. The only question is how much to pay in dividends. We want to choose the $D$ that maximizes:

Taking the derivative of $V$ with respect to $D$ and setting it to zero yields

In this way, we show that for cash-rich firms $\tau_c$ reduces corporate investment, but $\tau_d$ does not. This is considered quite counterintuitive since both $\tau_d$ and $\tau_c$ ultimately reduce the income of investors.

Conversely, cash-constrained firms don't pay dividends ($D=0$) and repeating the above optimization for them yields

which shows that both $\tau_d$ and $\tau_c$ reduce how much these cash-constrained firms will raise.

Turning to optimization, both firms and the government have effectively linear utility functions, so we represent overall social welfare as just their sum:

where $P_d$ is the net present value of the dividends:

We can compute the deadweight loss as:

Note that $\epsilon_{P_d}$ is 0 and positive depending on whether the firm is cash-constrained. Note: when we do similar analysis with $\tau_c$, we don't see this ambiguity: $\tau_c$ always creates deadweight loss.

The Agency Model

Empirical evidence suggests that the elasticity between dividend taxes and dividends are around 0.5, generally supporting the cash-constrained model. However, how much cash firms had on end did not predict their elasticity, suggesting that the neoclassical model doesn't actually predict firm behavior well.

On the other hand, we have decent evidence that firm's responses are affected by the incentives of the firm's top executives. In particular,

• When top executives hold a large proportion of the shares, the firm is more responsive to the dividend tax rate.
• When top executives hold a large number of stock options relative to overall shares, the firm is less responsive.
• When a firm's shares are largely owned by institutional investors, those investors can fight back against corrupt executive behavior, and we predictably find such firms are more responsive to changes in dividend tax rates.

Together, all these observations suggest treating executives as share-maximizers is pretty inaccurate. The main competing view is the "agency view".

This is further supported by comparing how C- and S-corporations responded to the 2003 dividend tax cuts Yagan. The study shows that the tax cut promoted payouts to shareholders but did not increase investment or employment.

One model is that the CEO has some pet project that they can direct investment to that yields personal utility $g(J)$ so their overall utility is given by

where $\alpha$ is the percent of the company they own.

This ends up entailing that the firm will still invest the optimal amount, but it will then take some of the money that should have gone to dividends and instead direct it to the CEO's pet project such that

In this way, we can conclude dividend taxes increases pet project spending at the expense of dividends while corporate income taxes reduces investment while leaving pet project spending unaffected.

However, the pet project deadweight loss is first-order while the investment deadweight loss is linear, so this suggests taxing dividends is more distortionary than taxing corporate profits - the opposite of the neoclassical model.

Dividends vs Share Repurchases

Prior to the 2002 tax-cut, dividends were taxed as ordinary income while capital gains were taxed at a lower rate. Given this, why did firms ever pay out dividends? The two primary theories are:

First, it's worth pointing out that at least until 1982, executives avoided stock buybacks due to fears of prosecution for market manipulation.

• Agency: Dividends act as a commitment to pay out your profits. Otherwise, executives and managers are motivated to retain this money to pursue personally beneficial projects Jensen.
• Signalling: Paying dividends signals that you have lots of money to burn.

These these two theories can be discriminated between by looking at how dividend announcements interact with tax rates when predicting stock price movements. In particular, the agency theory predicts that when taxes are high, dividend announcements will yield smaller stock price movements; the signalling theory predicts that the higher taxes will cause a larger stock price movement (since the signal is even more impressive). Empirically, the signalling theory looks stronger Bernheim.

One question is how to determine what the marginal dividend tax rate is.

This isn't because since the EMH predicts that since some people have a dividend tax rate of 0% (pension funds, the poor) there should be no dividend tax revenue (through complicated financial shenanigans, it can be arbitraged away). In practice, things aren't quite this extreme, but this kind of arbitrage makes naive averaging ineffective.

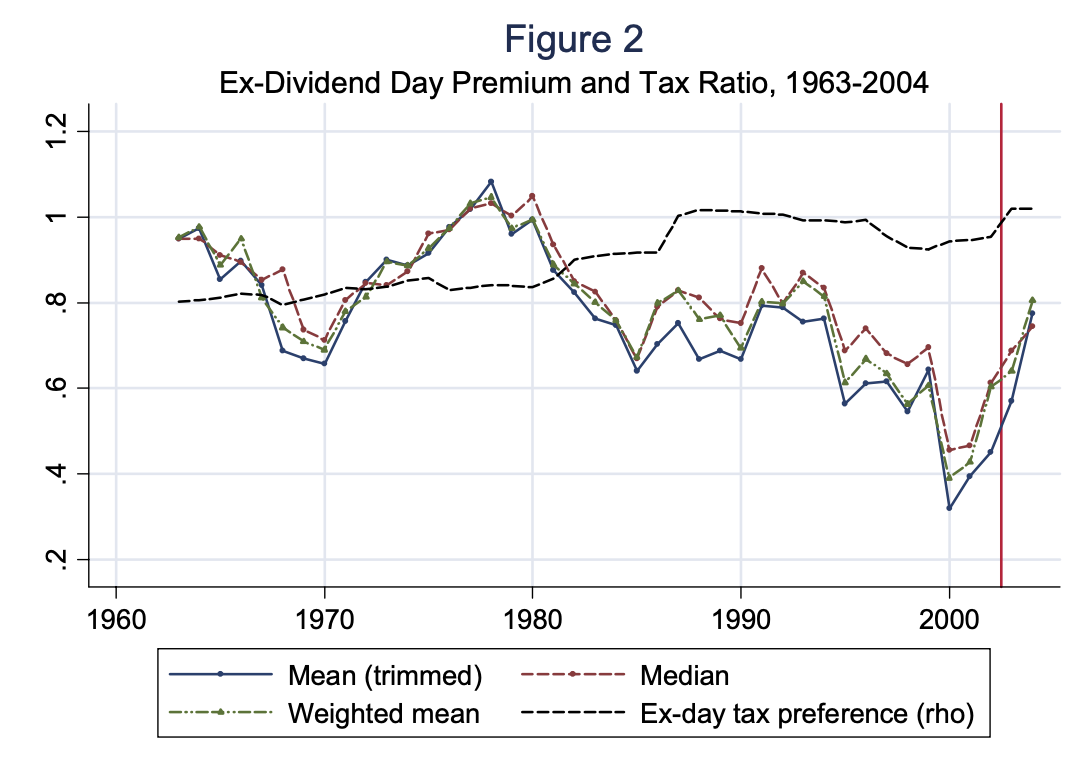
One way to figure this out is to take advantage of the fact that, if I buy your stock on the day a dividend is paid out, the dividend will still go to you (google "ex-dividend date"). We can take advantage of this and stock market efficiency assumption to compute the implied ratio between the $(1-\tau_d)$ and $(1-\tau_k)$ (the capital gains tax). This analysis yields a graph like

Corporate Profit Tax Elasticity

Like when estimating the elasticity of labor and taxes, we can estimate the elasticity of corporate profit and taxes using analysis of kinks and analysis of quasi experiments.

However, because firms have lots of flexibility in how they record expenses and profits, it's unclear how well these changes in reported corporate profits actually track the things we care about (mainly investment).

Depreciation Rules

When you buy things that last for years, you legally must deduct its depreciation each year rather than its whole value the first year. This harms firms, because it reduces the write-off's net present value.

Mathematically, we can represent the value to the firm of an investment with

where $z$ represents the proportion of the capital I can deduct on my taxes this year.

Optimizing with respect to $I$ yields

The right side is called the "user cost of capital" and is typically denoted as $c$.

Note that if $z=1$ (i.e. when we let firms deduct the year they buy the asset), there is no distortion.

This thinking led to a push for corporate tax reform to tax just the cash-flow - that is to effectively not tax profits that are re-invested. There's also an argument for this based on the ideal of taxing corporate rents Auerbach.

In any case, whether or note we set $z=1$, it does seem clear that increasing $z$ will incentivize investment. This and political motives have made it a tool for fiscal stimulus, which provides quasi experiments to analyze. One study estimates found very high elasticities (~6) House, indicating that firms will perform investment much sooner in response to these tax incentives, which indicates such policy is quite effective short-term stimulus ($1 of lost revenue causes $6 in investment). Other work suggests the impact could be larger if the tax changes targeted cash-constrained companies (e.g. smaller ones).

Interest vs Dividends

We currently let firms deduct interest from their profits but not their dividends. To examine how this affects their decisions, let's return to the neoclassical model.

Let $\rho$ be the interest rate and let's consider the last dollar invested before $\rho = f'(I)$. The net return from financing with debt is

where $\tau_z$ is the individual income tax on interest income. The net return from financing with equity is

where $\tau_e$ is the effective tax rate on equity payout. This implies debt is preferred iff

This predicts that either all money in a country will be raised with equity or that it will all be raised with debt. In the US, this shows debt if tax-favored in the US, so this is somewhat paradoxical.

Some proposed solutions include

• Firms can't deduct interest payments if they exceed earnings. While firms can carry these deductions forward, this is costly because (a) it has lower net present value and (b) your firm might go out of business.
• The effective tax rate on on equity could be low due to the arbitrage effects of buying shares around dividend payouts (discussed earlier).
• Debt and equity aren't perfect substitutes: (a) they have different risk profiles (b) managers become risk-seeking when working for a limited-liability firm (c) managers don't like debt because its stressful.

International Taxation

When a firm makes money abroad and brings the money back to the US, we allow the corporate income taxes paid to the foreign country to be subtracted from the corporate taxes you owe the federal government. Moreover, you can invest from these accounts into other foreign countries at will, which removes most of the incentive to bring the money back to the US. Finally, the government has occasionally created tax holidays for bring foreign earnings home. All of these factors have cause trillions of dollars owned by US companies to remain abroad.

The natural question is what the elasticity between this profit shifting and tax rates is. Quasi-experiments suggest the elasticity is fairly high, but that nearly all that money is given to investors in dividends and buybacks and the firms use very little to make new investments or employ more people. However, the shareholders have to either spend or save the money from these payouts, and the study didn't look into that part Dharmapala.