Resnet
Deep Residual Learning for Image Recognition was the 2015 paper that introduced the family of models known as "ResNet". The key idea was that by adding layers' outputs together at regular intervals, models could train better — presumably because the gradient flowed more directly through the network.
They start with the observation that it's entirely possible to create deeper networks (with more parameters) that, nonetheless, have higher training error (they give an example of a 20 layer network and a 56 layer network). This suggests that, while much progress had been made between 2012 and 2015 in network optimization (e.g. with batch normalization and smarter initialization schemes) these deeper models remained difficult to optimize.
They propose the intuition that networks should be easily able to represent the identity mapping -- this guarantees that the 56-layer model should never be worse than the 20-layer model, since it can learn the same 20 layers and then just learn an identity mapping. To achieve this they add "residual connections" every two layers, using "projection shortcuts" when the number of channels changes.
xi+1 = layeri(xi)
xi+2 = layeri+1(xi+1) + Wsxi
(where Ws is the fixed identity matrix of the dimensions don't change)
By inserting residual connections they get the 56 layer training error below the 20 layer network. They also propose a 34-layer, 50-layer, 101-layer, and 152-layer network, with each one achieving lower and lower training error. Due to practical considerations, the 50+ layer networks uses a 1x1 bottleneck and inserts residual connections every three layers instead of every two.
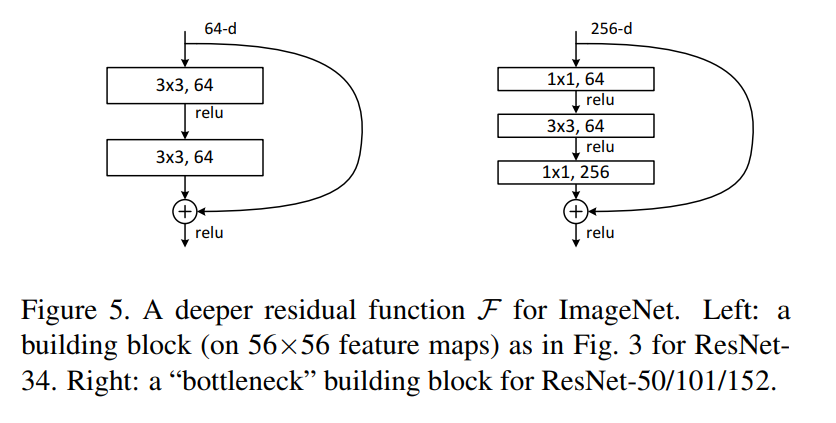
The 50, 101, and 152 layer networks are more accurate than the 34-layer one:
| ImageNet Results | |
| model | top-5 error |
| VGG-16 | 9.33% |
| GoogLeNet | 9.15% |
| PReLU-net | 7.38% |
| ResNet-34 | 7.46% |
| ResNet-50 | 6.71% |
| ResNet-101 | 6.05% |
| ResNet-152 | 5.71% |
Instead of using projection matrices, they also try simply zero-padding the additional channels, but find performance slightly degrades (top-5 error on ImageNet increases from 7.46% to 7.76%). Using learned (vs identity) projection matrices when the dimensions don't change also helps slightly.
The authors also train a 1202-layer network on CIFAR to 0.1% training error on CIFAR-10, showing that residual connections permit the optimization of absurdly deep networks.