Alexnet
Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097-1105).Dataset
The authors trained the subset of ImageNet used by the ILSVRC. It has 1.2 million images and 1000 categories. They downsampled their images to be 256x256 pixels.
Architecture
The network contains 8 layers, 5 convolutional followed by 3 fully connected. Each layer is succeeded by a ReLU activation function. Three of the convolutional layers use max pooling and two use response normalization.
Probably the weirdest feature of this network are the design decisions meant to support splitting the model across two GPUs. [This is rarely done anymore]. In its third, fourth, and fifth layers, Alexnet creates two independent sets of channels, each of which runs on a single GPU. These channels can only interact on layers 1, 3, and 6-8 (the fully connected layers).
The diagram provided in the paper is
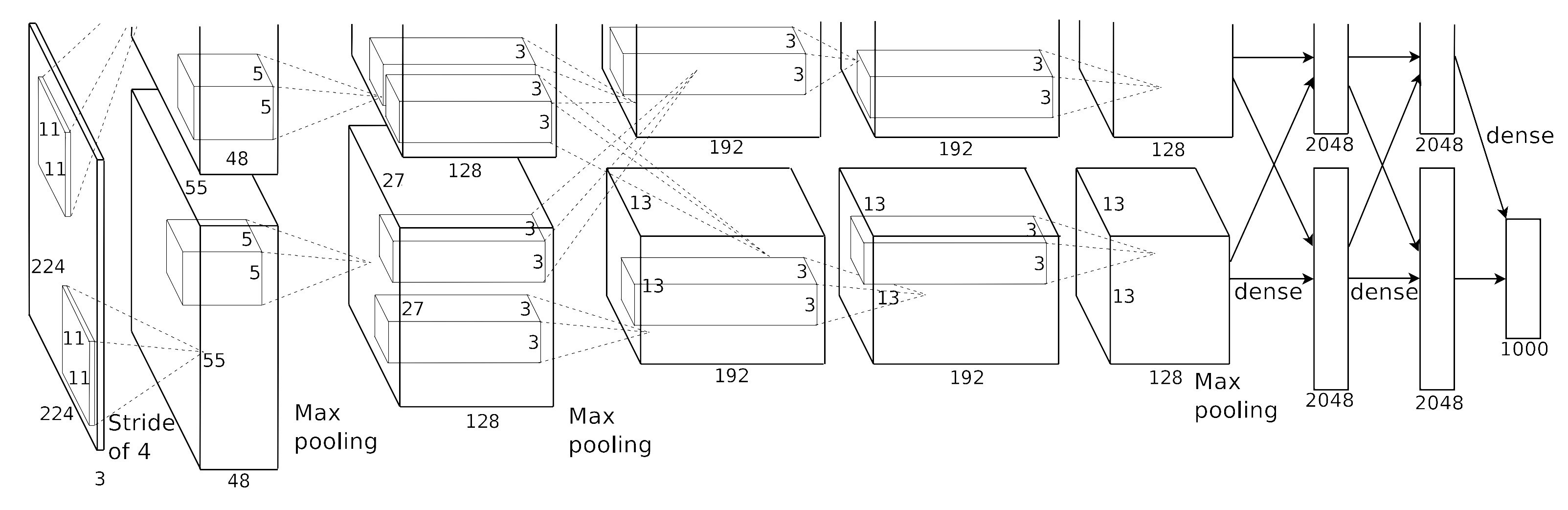 but I prefer this one:
but I prefer this one:
| Layer | GPU 1 | GPU 2 | Channels |
| 1 | 11 x 11 Convolution | 96 | |
| ReLU | |||
| Response Normalization | |||
| Max Pooling | |||
| 2 | 5 x 5 Convolution | 5 x 5 Convolution | 128 x 2 |
| ReLU | ReLU | ||
| Response Normalization | Response Normalization | ||
| Max Pooling | Max Pooling | ||
| 3 | 3 x 3 Convolution | 384 | |
| ReLU | |||
| 4 | 3 x 3 Convolution | 3 x 3 Convolution | 192 x 2 |
| ReLU | ReLU | ||
| 5 | 3 x 3 Convolution | 3 x 3 Convolution | 128 x 2 |
| ReLU | ReLU | ||
| Max Pooling | Max Pooling | ||
| 6 | Fully Connected (4096 neurons) | N/A | |
| ReLU | |||
| 7 | Fully Connected (4096 neurons) | N/A | |
| ReLU | |||
| 8 | Fully Connected (4096 neurons) | N/A | |
| ReLU | |||
- They use ReLU instead of tanh or sigmoid. They aren't the first do this, but they show that ReLu train several times faster than tanh units.
- They spread the net across two GPUs and claim this reduces their top-1 error rate by 1.7%.
- They implemented the Response Normalization despite the fact that ReLUs don't need it to avoid saturating. They say that doing so aids in generalization. The normalize in an odd way. Consider an activation at $(x,y)$ in some particular channel. Now consider the set of points in the same channel inside an $n \times n$ square centered on $(x,y)$ anad sum the square of their activations, call this $S$. They then divide the activation at at $(x,y)$ by $\left(k + \alpha S\right)^\beta $, where $k$, $\alpha$, and $\beta$ are hyper-parameters (they use $k=2$, $n=5$, $\alpha=10^{-4}$, and $\beta=0.75$. They find this reduces their top-1 error rate by 1.4% and that this reduces error on CIFAR-10 too.
- They use overlapping pooling. Traditionally, pools didn't overlap, but they found overallping pools reduced top-1 error by 0.4%.
Reducing Overfitting
- They select sub-patches from images and apply horizontal reflections to generate more data.
- They apply minor linear transformations to the RGB values in the image, which reduces their top-1 error by over 1%.
- The use dropout with $p=0.5$.
Other Details
They used stochastic gradient descent:- Batch Size: 128
- Momentum: 0.9
- Weight Decay: 0.0005
In particular, they found the small weight decay to be very important.
The initalized each weight with $N(0,0.01)$. The initialized the weights of layers 1 and 3 with biases of 0 and the remaining layers with biases 1. The non-zero bias terms accelerates early stages of learning by giving ReLUs more non-zero gradients.
They started the learning rate at 0.01 and manually adjusted it down by a factor of ten three times - each adjustment was made once validation error stopped decreasing. They completed 90 cycles over 5-6 days.
In terms of accuracy, Alexnet provided state-of-the-art results and generalized well to related image classificaiton problems.
One unexpected result from their 2-GPU model is that one GPU paid a lot of attention to color, while the tended to ignore it - a result resiliant to the weight initializations.